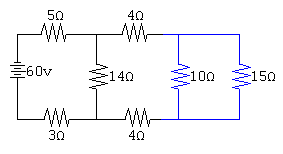
Problem 9: A
60V potential difference is applied to the circuit shown below. Find the
current in 10Ω resistor.
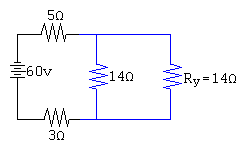
After replacing Rx in the circuit, Now Rx, and two 4Ω resistors are in series combination, so their equivalent Ry will be:
Now Ry and 14Ω resistors are in parallel combination, so their equivalent resistance (Rz) will be:
Now all resistors are in series, so their equivalent resistance will be:
Since Rz was the parallel combination of Ry and 14Ω resistors. So voltage across each resistor will be same as that of Rz. So voltage across Ry will be:
Ry was the series combination of three resistors, so each resistor will have same current as that of Ry resistor. So current across Rx will be:
Since Rx was the combination of two parallel resistors, so each will have same voltage as that of Rx resistor. So voltage across 10Ω resistor will be:
Step: 1 Overview
Parallel Combination of resistors.See overview of problem 7.Series combination of resistors.
See overview of problem 8.
Step: 2 Calculation
10Ω and 15Ω resistors are in parallel combination, so their equivalent (Rx) will be:
1/Rx=(1/10)+(1/15)Now replacing Rx in the place of 10Ω and 15Ω resistors.
1/Rx=(3+2)/30
1/Rx=5/30
Rx=30/5
Rx=6Ω
After replacing Rx in the circuit, Now Rx, and two 4Ω resistors are in series combination, so their equivalent Ry will be:
Ry=Rx+4+4Now replacing Ry in the place of three series resistors.
Ry=6+4+4
Ry=14Ω
Now Ry and 14Ω resistors are in parallel combination, so their equivalent resistance (Rz) will be:
1/Rz=(1/Rx)+(1/14)Now replacing Rz in place of parallel resistors.
1/Rz=(1/14)+(1/14)
1/Rz=2/14
Rz=14/2
Rz=7Ω
Now all resistors are in series, so their equivalent resistance will be:
R=Rz+5+3Now total current will be:
R=7+5+3
R=15Ω
I=V/RSince Rz, 5Ω and 3Ω resistors are in series, so current in each resistor will be same, which is equal to total current. So current in Rz will be:
I=60V/15Ω
I=4A
Iz=4AAnd voltage across Rz will be:
Vz=IzRzNow going back to more complex circuit:
Vz=(4)(7)
Vz=28V
Since Rz was the parallel combination of Ry and 14Ω resistors. So voltage across each resistor will be same as that of Rz. So voltage across Ry will be:
Vy=28VAnd current across Ry will be:
Iy=Vy/RyNow again going back to even more complex circuit consisting of Rx resistor:
Iy=28/14
Iy=2A
Ry was the series combination of three resistors, so each resistor will have same current as that of Ry resistor. So current across Rx will be:
Ix=2ANow voltage across Rx:
Vx=IxRxNow coming to the orignal circuit:
Vx=(2)(6)
Vx=12V
Since Rx was the combination of two parallel resistors, so each will have same voltage as that of Rx resistor. So voltage across 10Ω resistor will be:
V10=12VBut we need to find current across 10Ω resistor, so current will be:
I10=V10/R10
I10=12V/10Ω
I10=1.2A (Ans)